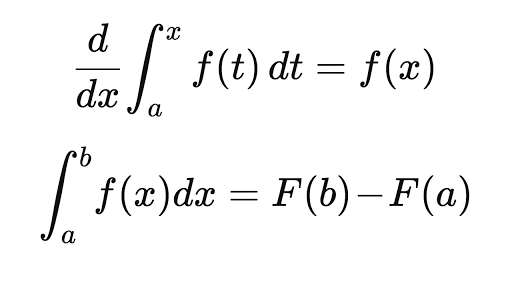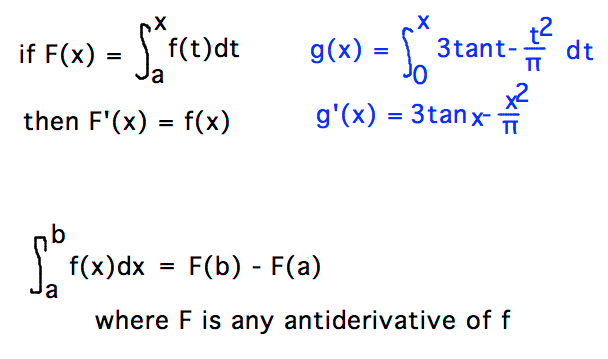How To Take The Derivative Of An Integral With Bounds

As expected the definite integral with constant limits produces a number as an answer and so the derivative of the integral is zero. When talking about the derivative and a definite integral we need to talk about the fundamental theorem of calculus. The definite integral of a function on a given interval is defined as the area under the.

how do you take your blood pressure without a machine how do you take your own passport photo at home how do you take live photos how do you take iron pills how do you take lipozene and metaboup how do you take off fake nails without acetone how do you take in the waist of jeans how do you take notes on ipad pro

Download VPN

Taking Derivatives Of Integrals Youtube

$Leibniz Integral Rule Wikipedia$

Download VPN

Leibniz Integral Rule Wikipedia

Download VPN

Differentiation Of Definite Integrals With Variable Limits Youtube

Download VPN

Derivatives Of Integrals W Chain Rule Youtube

Download VPN

Solved Derivative Of A Integral With Two Function Bounds

$Leibniz Integral Rule Wikipedia$

Download VPN

Leibniz Integral Rule Wikipedia

Compute the derivative of the integral of f x from x 0 to x 3.

How to take the derivative of an integral with bounds. Let f x e x 2. Compute the derivatives of the two integrals. 2 in the algebraic simplification to tidy up the answer we use the fact that cos x is positive for x in the interval π 4 x π 4 to conclude that cos 2 x cos x. X is on both bounds definite integrals properties review.

The hotkey for the integral without limits is ctrl i and the hotkey for the integral. Interactive graphs plots help visualize and better understand the functions. The integral calculator supports definite and indefinite integrals antiderivatives as well as integrating functions with many variables. We then have our original function.

Derivative or integral operation. Compute the derivative of the. If you re seeing this message it means we re having trouble loading external resources on our website. Let f x 3x 2.

We also recognize the. 1 the chain rule is used to find both derivatives. The derivative of a definite integral. For more about how to use the integral calculator go to help or take a look at the examples.

Remove answer to the above step notes. This video shows how to use the first fundamental theorem of calculus to take the derivative of an integral from a constant to x from x to a constant and from a constant to a function of x. Finding derivative with fundamental theorem of calculus. With limits is ctrl.

X is on lower bound finding derivative with fundamental theorem of calculus. The definition of definite integral is much more intuitive that that of an indefinite integral. You can also check your answers. From the first part of the theorem g x e sin2 x when sin x takes the place of x.

From chain rule we take the derivative of the outside function g times the derivative of the inside function sinx. Here are two examples of derivatives of such integrals. Sometimes you need to swap the bounds of integration before applying the fundamental theorem of calculus. One approach is to first define the function and then enter a separate function for the.

We take the derivative of both sides with respect to x. Note that the derivatives are performing partial.